Hoeveel participanten moet ik werven voor mijn onderzoek?
Mathijs Deen, statisticus/methodoloog
In deze tutorial wordt aan de hand van een drietal voorbeelden uitgelegd hoe je erachter komt hoeveel participanten je moet werven voor je wetenschappelijk onderzoek. Het programma G*Power, dat je hiervoor kunt gebruiken, wordt uit de doeken gedaan.
Een veelgestelde vraag voorafgaand aan een wetenschappelijk onderzoek is, hoeveel participanten er geworven moeten worden. Als je onderzoek WMO-plichtig is, en je dus voor goedkeuring langs de Medisch Ethische Toetsingscommissie (METC) moet, wordt hier altijd om gevraagd. Ook wanneer je je onderzoek i.h.k.v. een opleiding doet, is het gebruikelijk dat je de door jou gekozen steekproefgrootte beargumenteert. Voor de berekening van je steekproefgrootte kun je binnen Parnassia Groep gebruik maken van het programma G*Power. Voor dit programma kun je geautoriseerd worden via je leidinggevende of je teamrolhouder personeel. Duurt dat je te lang, heb je daar geen trek in, vind je je leidinggevende doodeng of heb je andere redenen om het niet via het PG-netwerk te doen, dan kun je de software ook gratis voor je eigen pc/Mac downloaden via http://www.gpower.hhu.de/en.html.
Hieronder leg ik je aan de hand van twee eenvoudige en een wat ingewikkeldere casus uit hoe G*Power werkt en waar je op moet letten bij het berekenen van je steekproefgrootte. Omdat “statistische power” (waarover hieronder meer) één van de elementen is in de berekening, wordt deze berekening ook wel “poweranalyse” genoemd.
Een eenvoudig voorbeeld: de onafhankelijke t-toets
Stel, we willen onderzoeken of mensen met een histrionische-persoonlijkheidsstoornis en mensen met een cluster c-persoonlijkheidsstoornis van elkaar verschillen in de mate van extraversie. Je zou dit kunnen onderzoeken door twee groepen mensen te vergaren: een groep mensen met de histrionische- en een groep mensen met een cluster c-persoonlijkheidsstoornis (mensen in dit onderzoek voldoen vanzelfsprekend niet aan beide diagnoses). Je neemt bij deze mensen een vragenlijst af die extraversie meet, en de uitkomstmaat die je hebt is een continue totaalscore voor de mate van extraversie. Je besluit dat je na afloop van de dataverzameling het verschil tussen de twee groepen wilt gaan toetsen d.m.v. een onafhankelijke t-toets. Nu rijst de vraag: “ok, maar hoeveel mensen heb ik dan nodig?” Dit is het moment waarop we G*Power inschakelen.
Als je G*Power opent, zie je een scherm dat er ongeveer zo uit ziet:
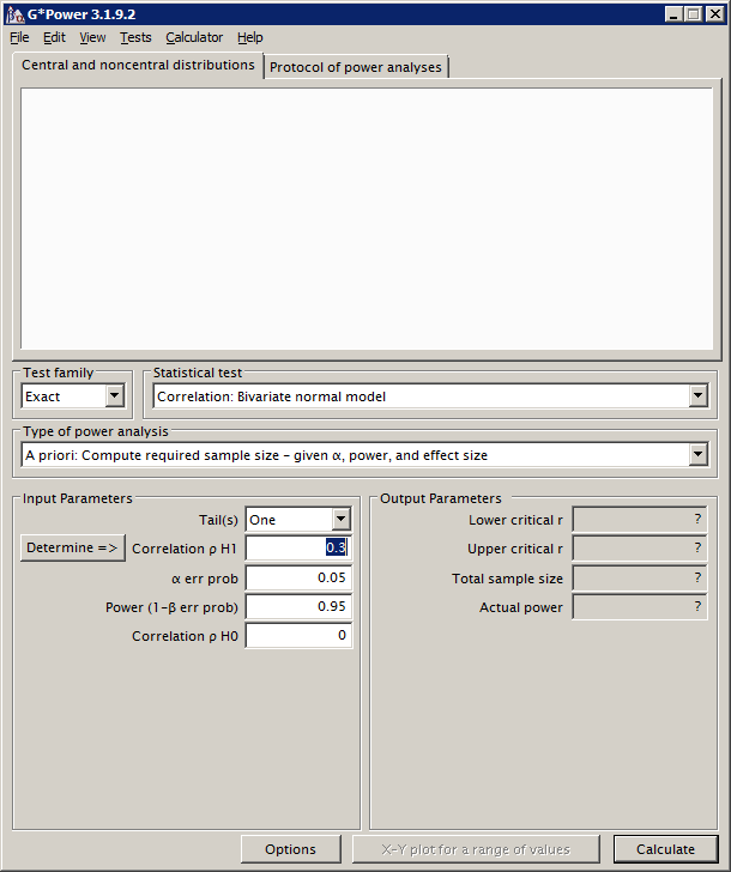
Het grote witte vlak kunnen we voor nu even negeren, hier wordt later een grafiek in getekend (de grafiek die hier komt, kun je later overigens ook negeren…). We zien nogal wat menu’s en waardevelden waar we e.e.a. kunnen selecteren en invullen. Het is van belang om te weten dat de berekening voor de steekproefgrootte afhangt van de statistische test die je wilt uitvoeren. Hierboven hadden we al geconcludeerd dat we een onafhankelijke t-toets willen doen. Nu maakt G*Power onderscheid tussen een aantal zogenaamde testfamilies. Hier kunnen we kiezen uit Exact, F test, t test, χ2 test en z test. O.b.v. je keuze in het vakje “Test family” kun je in het vak ernaast een statistische toets uit die familie kiezen. Voor een statisticus is het logisch welke test nou onder welke familie valt, voor niet-statistici is het soms een kwestie van zoeken. De t-toets vinden we, je raadt het al, bij de familie “t test.” Als je deze familie selecteert, kun je bij Statistical test kiezen voor “Means: Difference between two independent means (two groups).” We hebben immers twee groepen, en we willen het verschil in gemiddelden toetsen. Voor ons doel (het van te voren bepalen van de steekproefgrootte) kunnen we in het veld eronder “A priori: Compute required sample size (…)” laten staan. Nu volgt de input.
De input verschil per statistische test. In dit geval kunnen we ten eerste kiezen of we één- of tweezijdig willen toetsen. Ik ga in deze tutorial verder niet in op het verschil tussen die twee, maar zeg alleen dat er de laatste jaren steeds meer mensen tegen éénzijdig toetsen zijn, omdat dit tot frauduleuze onderzoekspraktijken kan leiden. Voor nu volstaan we door te kiezen voor tweezijdig toetsen (Tail(s) zetten we dus op “Two”).
Effect size: Cohen’s d
Het volgende veld gaat over de effect size, en in het geval van de t-toets is dit gewoonlijk Cohen’s d. We moeten ons nu een idee verschaffen van hoe groot we verwachten dat het verschil tussen de twee groepen is, uitgedrukt in Cohen’s d – dus in aantal standaarddeviaties. Nu is dit vaak problematisch: dit weten we vaak niet, en dat is nou precies waarom we dit onderzoek doen. Als je geen idee hebt van de effect size die je verwacht, is het verstandig om van een effect size uit te gaan waarvan je vindt dat het de laagste interessante waarde is. Dus een waarde waarvan je denkt “nou, als het effect nog kleiner is dan dit, dan vind ik het eigenlijk niet meer een wezenlijk effect”.
Er worden voor effect sizes in het algemeen vaak standaardwaarden gebruikt zoals die te vinden zijn in het standaardwerk van Jacob Cohen (1988). In het geval van Cohen’s d spreekt men vanaf 0.20 van een klein effect, vanaf 0.50 van een middelmatig effect, en vanaf 0.80 van een groot effect. Het is aan te raden om zoveel mogelijk zelf een idee te krijgen van een wezenlijke effect size voor jouw onderzoek, gebaseerd op de gemiddelden die je verwacht (of die je minimaal interessant vindt), en de standaarddeviaties van de groepen. Alleen als je hier zelf werkelijk geen enkele onderbouwing voor een specifieke effect size voorhanden is. Voor het vervolg van dit voorbeeld gaan we uit van een Cohen’s d van 0.80.
Alpha
Hierna vullen we de alfa-waarde in, zeg maar je kritieke p-waarde. Gewoonlijk is dit .05, oftewel: bij p-waardes kleiner dan .05 spreken we van statistische significantie. Soms moet je deze waarde echter verkleinen. Stel nou dat we extraversie op twee verschillende manieren meten: met de NEO-PI-R en met de Big Five Inventory, dan toetsen we eigenlijk dezelfde hypothese twee keer: met elk van de uitkomsten een keer. Maar, dan is er sprake van wat we noemen kanskapitalisatie: je krijgt een grotere kans dat je bij toeval een p-waarde onder de .05 vindt (wanneer er in werkelijkheid geen verschil is tussen de groepen). Een gebruikelijke manier is om hiervoor te corrigeren d.m.v. een Bonferroni-correctie. Je alpha maak je dan twee keer zo klein – je deelt die gebruikelijke .05 door het aantal keer dat je de hypothese met verschillende operationalisaties van je afhankelijke variabelen toetst. Je wordt dan dus strenger wat betreft je beoordeling van statistische significantie. Voor nu laten we hem op .05 staan.
Power
Dan komt de power. Hier kunnen we kort over zijn: deze staat eigenlijk altijd op .80. Dit is de kans dat je statistische toets een groepsverschil vindt in je steekproef met \(p<.05\), gegeven dat dit verschil in de gehele populatie daadwerkelijk aanwezig is. Je wilt natuurlijk niet dat een daadwerkelijk aanwezig verschil niet gevonden wordt in jouw onderzoek – de kans hierop wordt echter groter bij een kleinere steekproef. Hoe meer power, hoe meer participanten je nodig hebt. En vice versa.
Allocation ratio
Dan is er specifiek voor de t-toets nog de mogelijkheid om de groepsgroottes qua verhouding te laten verschillen, in het vakje “Allocation ratio N2/N1”. Hoeveel groter mag groep 2 zijn, t.o.v. groep 1? Stel, in ons voorbeeld, dat we denken dat we moeilijk mensen met de histrionische-persoonlijkheidsstoornis zullen vinden, dan kunnen we er voor kiezen om bijvoorbeeld twee keer zoveel mensen te werven in de andere groep. In dat geval vullen we in dit veld “2” in. Let wel: hoe meer deze ratio afwijkt van 1 (groepen zijn dan even groot), hoe meer mensen je in totaal nodig zult hebben. Voor nu laten we hem op 1 staan.
Nu hebben we de gegevens ingevuld, en kunnen op de knop “Calculate” klikken. Je scherm ziet er dan als volgt uit:
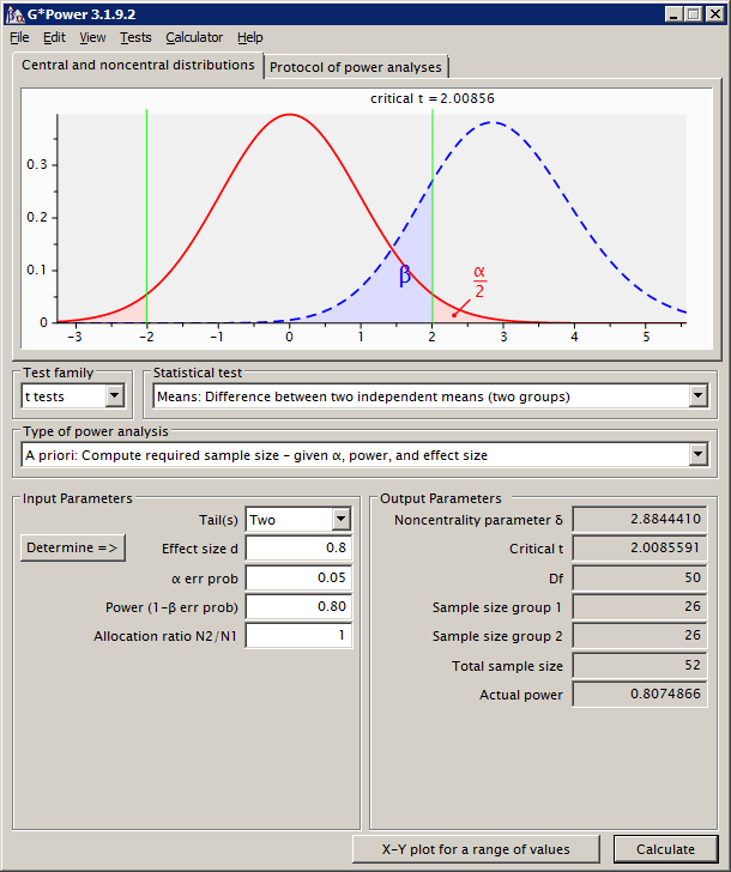
De benodigde steekproefgrootte
Blijkbaar hebben we twee groepen van 26 participanten nodig, in totaal dus 52 mensen. Klik je op het tabblad “Protocol of power analyses”, dan krijg je de in- en uitvoer van je huidige poweranalyse, en eventuele eerdere poweranalyses, te zien, die je in een ander bestand kunt plakken voor reproduceerbaarheid van je berekening.
Nog een voorbeeld: de Pearsoncorrelatie
Stel, we willen om de één of andere reden weten wat de correlatie is tussen extraversie en emotieregulatie. Extraversie is gemeten met de NEO-PI-R, en emotieregulatie met de SIPP-118. Uit beide vragenlijsten komen continue schalen naar voren, en dan kunnen we een Pearson product-momentcorrelatie (kortweg: Pearsoncorrelatie) berekenen. Nou verwachten we een sterk verband, zeg r = .50. Hoeveel mensen moeten we includeren om deze correlatie statistisch significant (\(p < .05\)) te laten zijn, met een power van .80? G*Power weet raad.
We klikken bij “Test family” op “Exact” en kiezen als statistische test “Correlation: bivariate normal model”. We gaan er van uit dat beide variabelen een normale verdeling volgen. We toetsen ook hier tweezijdig, en vullen onze verwachte correlatie van .50 in het volgende veld in. Alpha en power zetten we wederom op .05 en .80. Nu zien we een veld “Correlation ρ H0,” die standaard op 0 staat. In dit veld vullen we de correlatie in zoals we die onder de nulhypothese verwachten. De nulhypothese zegt “er is niks aan de hand,” wat in dit geval betekent “de correlatie is er niet, hij is 0.” De waarde 0 kunnen we dus laten staan. Theoretisch zou je hier dus een andere nulhypothese kunnen hanteren (in de praktijk zul je dit niet zo snel doen). Voor deze specificatie zouden we 29 mensen moeten includeren.
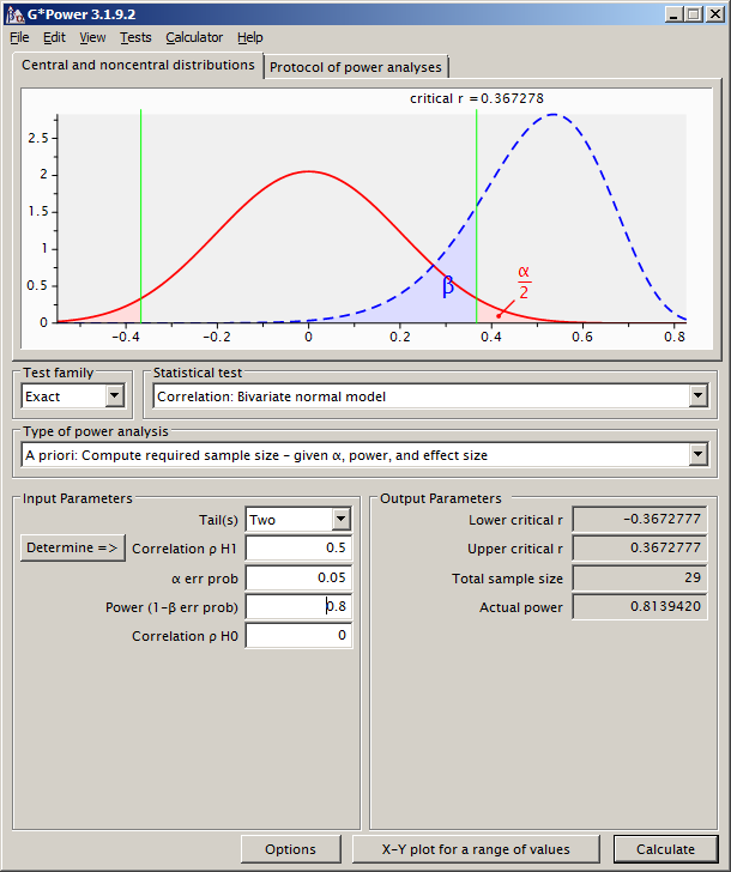
Misschien wel goed voor het verschaffen van wat meer inzicht in de relatie tussen effect size (hier de correlatie) en benodigde sample size: als we de verwachte correlatie verkleinen naar bijv. .30, dan ga je een groter aantal participanten nodig hebben (in dit geval: 80). In het algemeen geldt: je hebt meer mensen nodig als je een kleiner effect verwacht, als je meer power wilt hanteren, en als je een lager alfaniveau aanhoudt.
Een ingewikkelder voorbeeld: de ANOVA voor herhaalde metingen
Binnen Parnassia Groep doen we veel onderzoek naar effecten van behandeling. Bijvoorbeeld in Randomized Controlled Trials (RCT’s), waarin we onderzoeken of patiënten meer baat hebben bij een nieuwe, experimentele behandelmethode dan bij de gebruikelijke behandeling. Bijvoorbeeld: binnen een groep mensen met een eetstoornis en een laag zelfbeeld willen we onderzoeken of het lage zelfbeeld meer verbetert met Competitive Memory Training (COMET) dan met standaardbehandeling (vaak afgekort als TAU – Treatment As Usual). Bij iedere participant wordt vlak voor de start van de behandeling (T0), halverwege (T1), direct na afloop (T2) en drie maanden daarna (T3) de Self Esteem Rating Scale afgenomen, die het expliciete zelfbeeld meet.
Er zijn verschillende statistische technieken om data uit zo’n onderzoek te analyseren, voor nu beperken we ons tot de repeated measures ANOVA met “within-between interaction.” We hebben een within-subject factor tijd (de herhaalde metingen die iedere persoon heeft), en een between-subjects factor groep (participanten zitten in ofwel de experimentele ofwel in de standaardbehandeling). We willen weten of de experimentele groep over de tijd gemiddeld meer verbetert dan de gebruikelijke behandeling, wat bij de analyses tot uiting komt tot een interactie tussen tijd en groep. Verbetert het zelfbeeld bij de COMET-deelnemers meer dan bij de deelnemers die TAU krijgen?
Voor de repeated measures ANOVA kunnen we in G*Power een poweranalyse doen. Je vindt hem onder de F tests, en in dit geval gaan we bij “Statistical test” voor “ANOVA: repeated measures, within-between interaction.” Het valt op dat we, in vergelijking met de t-toets hiervoor, wat meer gegevens moeten invullen.
Effect size: Cohen’s f
Ik noemde eerder al dat verschillende statistische tests, verschillende effect sizes hebben. Om dat nog wat ingewikkelder te maken: specifiek voor de ANOVA’s zijn er ook nog eens een stuk of vijf in omloop: Cohen’s f, Cohen’s \(f2\), \(\omega^2\), \(\eta^2\) en partial \(\eta^2\). Meestal wordt de laatstgenoemde gerapporteerd, omdat deze standaard uit de statistieksoftware komt rollen die misschien wel het populairst is bij mensen die repeated measures ANOVA’s doen (te weten: SPSS). Nu wil G*Power echter Cohen’s f hebben. Geen nood, we kunnen de partial \(\eta^2\) laten omrekenen naar deze maat. Hiertoe klikken we eerst onder de knop “Options” de optie “as in SPSS” aan, en klikken daarna, links van het Effect size veld, op de knop “Determine =>.” Er plopt rechts een schermpje tevoorschijn, waar je onder het kopje “Direct” je verwachte effect size kunt invullen, uitgedrukt in partial partial \(\eta^2\). Voor deze maat is het wellicht wat moeilijker om een gevoel te krijgen voor wat je nou klein of middelmatig of groot of groot genoeg vindt. Zouden we teruggrijpen op de standaard afkappunten, dan gelden .01, .06 en .138 voor resp. een klein, middelmatig, en groot effect. We kiezen voor een medium effect, en laten de omrekening “transferren” naar het hoofdscherm, waar de waarde 0.2526456 wordt ingevuld voor de effect size.
Alpha en power
Deze waardes zijn hetzelfde als bij de t-toets die we hiervoor behandelden: resp. .05 en .80.
Number of groups en Number of Measurements
Deze waardes zijn ook niet zo lastig te bepalen: we weten dat we twee groepen hebben, en vier meetmomenten. Dit hebben we zelf verzonnen, en vullen we dan ook in.
Nonsphericity correction \(\epsilon\)
Sfericiteit is een assumptie van de repeated measures ANOVA. Zonder verder op die materie in te gaan: de nonsfericiteitscorrectie corrigeert voor de mate waarin je data niet voldoet aan deze assumptie. Gewoonlijk heb je hierover van te voren geen flauw idee, dus deze waarde is eigenlijk niet echt in te schatten. Laten we hem lekker op 1 staan.
De benodigde steekproefgrootte
Klikken we op de knop “Calculate” dan zien we dat we in totaal 62 participanten nodig hebben.
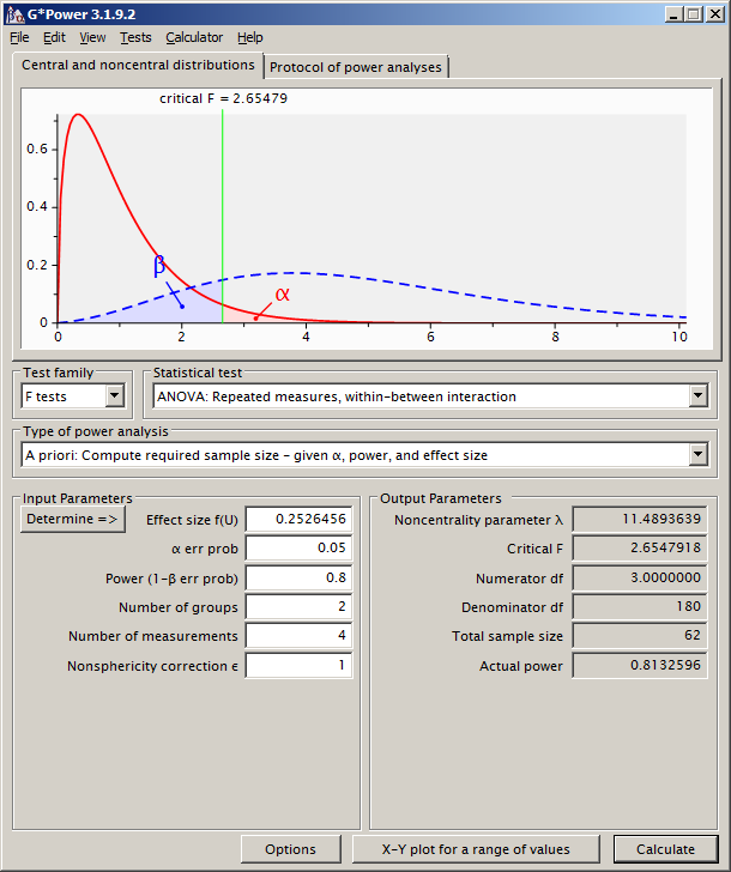
En hoe doe ik het nu zelf?
Ik heb je drie voorbeelden laten zien: twee eenvoudige en eentje die wat meer om het lijf had. Het lastigste zit hem denk ik in het inschatten van je effect size. Vaak weet je niet wat je moet verwachten, logisch, want dat is nou juist waarom je dit onderzoek doet. Maar, misschien kun je het hier eens over hebben met andere experts in je vakgebied, misschien hebben zij een idee. Soms kun je naar de resultaten kijken van eerdere studies, waarin een soortgelijk onderzoek is gedaan binnen een soortgelijke populatie. En soms heb je echt geen idee, dan komt het op een soort onderbuikgevoel aan. Probeer desalniettemin je gekozen waarde zo veel mogelijk te onderbouwen. En als het echt niet anders kan, kun je eventueel uitwijken naar de standaardwaarden die bij de effect size horen die op jouw toets van toepassing is. De overige parameters die je moet invullen zijn ofwel vrij standaard (alpha en power), of ze volgen als het goed is uit je design. En als je een inschatting hebt over of je nou een klein, een middelmatig of een groot effect hebt, dan weet je misschien voor jou specifieke analyse niet direct wat de afkappunten zijn.
Deze tutorial is natuurlijk niet alomvattend. Ik hoop wel dat het je handvatten geeft om een goede poweranalyse te kunnen doen. Nu is het zo dat, net als dit document, ook G*Power niet alomvattend is. Voor sommige analyses (bijv. mediatieanalyses, multilevelanalyses) biedt deze software geen soelaas. Neem even contact met me op als ik je hierbij kan helpen. Ook als je er niet uit komt, of aanvullende vragen hebt, laat het me gerust weten! Het kan ook zijn dat je je kapot schrikt van het waanzinnig hoge aantal participanten dat je volgens G*Power zou moeten gaan werven. Laat het me weten, misschien kunnen we wat in je design aanpassen of kijken wat er eventueel mis ging in je berekeningen.
Literatuur
- Cohen, J. (1988). Statistical power analysis for the behavioral sciences (2nd Ed). NJ: Lawrence Erlbaum Associates.